by James Richardson
From: Meteor Trails, Journal of the AMS, June 1999 (No. 4)
One of my favorite observation sites used to be a small clearing high in the Idaho Rockies, next to a winding mountain highway, and set above the sparse twinkling farmhouse lights of sleepy Arbon Valley. The viewing here was always spectacular, with the night sky arching overhead like the dome of some immense cathedral, the stars near the horizon nestled between mountain peaks and nearly as bright as those directly overhead. Set against this sparkling backdrop, the fleeting flashes of meteors appeared to be nearly as distant as the celestial dome itself, with those meteors at low elevation angles neither closer nor farther away than those directly overhead. Through my reading, I had learn that these objects were burning themselves up at altitudes of about 80-120 km (50-75 miles) in the Earth’s upper atmosphere, but it was difficult to translate this knowledge into some idea of actual distances when I was out observing in the field. The purpose of this article is to give the meteor observer some idea as to the shape and size of the layer of atmosphere in which their meteors occur, to provide a way for calculating meteor distances from the observer as a function of meteor zenith angle, and to use this information to briefly explore the nature of those most beautiful of meteors — the long, sky-crossing “Earth grazers.”
The Meteor Meniscus
Armed with the fact that the Earth has an equatorial radius of 6378 km, that meteors occur at between 80-100 km of altitude, and that the horizon for an observer on the surface of the Earth is a flat plane tangent to the surface of the Earth, we can construct a cross-sectional view of the area of the atmosphere in which meteors occur for a single observer. Figure 1 shows such a cross-sectional view, with all distances shown to scale.
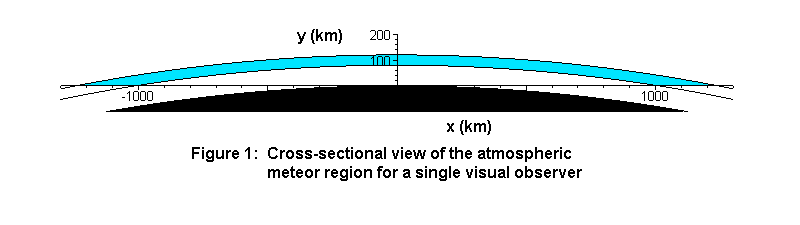
In this view, the observer is located at the origin of our coordinate system, with horizontal distances labeled on the X-axis and vertical distances labeled on the Y-axis. Directly beneath the observer is the solid Earth, very gradually rolling down to either left or right. Above the observer is the relatively thin layer of atmosphere (shaded in Grey) in which meteors occur, a layer which is very nearly flat directly overhead, but which gently curves down toward the horizon with increasing distance, slipping below it at between 1013 and 1243 km distance from the observer. If we mentally rotate this cross-sectional view 180 degrees about the Y-axis, we find that the layer of atmosphere in which our observer’s meteors occur forms a very flat spherical cap, or convex meniscus. That is, to use an analogy, rather than viewing our meteors imbedded in the transparent glass of a great, inverted “bowl” overhead, we instead view our meteors imbedded in the transparent glass of a great inverted “saucer” overhead. However, behind this transparent “saucer” of atmosphere sits the immense dome of the celestial sphere, making our flat meniscus of atmosphere difficult to visualize when out in the field.
Calculating Meteor Distance as a Function of Meteor Zenith Angle
Figure 2 shows a close-up view of the right hand quadrant shown in figure 1. Our goal is to determine the distance(d) from an observer (located at the origin) to a meteor occurring in the region bounded by the two solid lines (indicating atmospheric heights of 80 to 120 km), if we are given the atmospheric height of the meteor (h) and its zenith angle (z = 90 deg – altitude_angle), as shown in the figure.
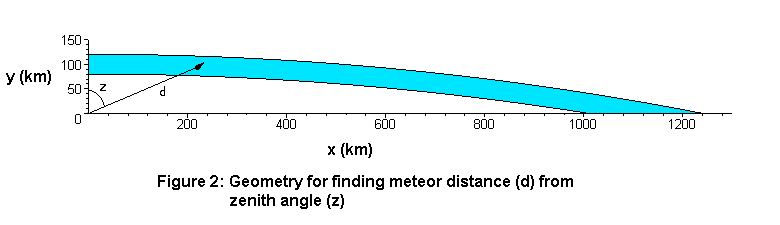
We find this distance (d) by forming the non-right triangle having the observer, the center of the Earth, and the meteor at its vertices. The distance between Earth center and the observer is the Earth radius at r=6378 km; the distance between Earth center and the meteor is r+h = 6458-6498 km); and the distance between the observer and the meteor is our desired range, d. Using the law of cosines, we can form the following relationship:
(r + h)^2 = r^2 + d^2 – (2 * r * d * cos(180 deg – z)
Solving for the distance, d, will yield the following equation:
d = sqrt(r^2 * cos^2(z) + 2*r*h + h^2) – r * cos(z), [Eq. 1]
where:
sqrt = the positive square root operator
r = 6378 km,
h = 80-120 km,
z = meteor zenith angle (deg),
d = meteor distance from the observer (km),
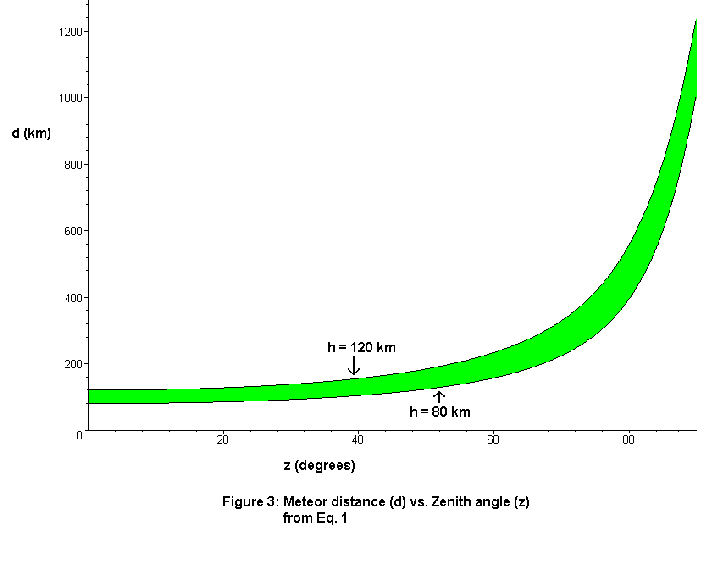
Using Eq. 1, Figure 3, above, shows meteor distances, d, on the Y-axis, plotted as a function of meteor zenith angle, z, on the X-axis. The two solid lines represent the boundaries formed by our meteor height range of80-120 km, with the higher meteors having greater ranges. This same information is presented in tabular form below:
Table 1: Meteor Distances for Selected Meteor Zenith Angles
| Zenith Angle (z) | Meteor Distance (d) |
|---|---|
| 0 deg | 80-120 km |
| 10 deg | 81-122 km |
| 20 deg | 85-128 km |
| 30 deg | 92-138 km |
| 40 deg | 104-156 km |
| 45 deg | 112-168 km |
| 50 deg | 123-184 km |
| 55 deg | 138-205 km |
| 60 deg | 157-234 km |
| 65 deg | 184-273 km |
| 70 deg | 224-239 km |
| 75 deg | 286-416 km |
| 80 deg | 394-557 km |
| 85 deg | 600-805 km |
| 90 deg | 1013-1242 km |
Of interest in this figure and table is the fact that meteor distances increase quite gradually over the first 45 degrees or so of zenith angle, but then increase quite rapidly over the remaining 45 degrees down to the horizon. This will have application later when we discuss (in a separate article) the effect of increasing meteor distances and atmospheric absorption on observed meteor magnitudes. Suffice it to say at this point that meteors within 30-40 degrees or so of the horizon will experience significantly more magnitude extinction than those more directly overhead, which also significantly decreases the number of meteors seen in the lower region. This is why most meteor observers generally keep the center of their gaze at between 45-70 degrees of altitude above the horizon — focusing their attention on the closer, brighter meteors.
The Meteor Distance First Order Approximation
Although the formula for meteor distance as a function of zenith angle given above is the correct one, it will not be encountered in most meteor astronomy textbooks. This is because for most applications, a much simpler first order approximation of this equation will function quite well in its stead. This approximation assumes a flat, planar Earth in the region of the observer, and a correspondingly flat, planar atmospheric meteor zone above this patch of Earth. This will allow us to form a right triangle between the observer on the ground, a meteor at some height (h) and zenith angle (z), and the point directly over the observer also at height h. This will yield the simple relationship:
d = h / cos(z) or d = h * sec(z) [Eq. 2]
At first glance, Eq. 2 bears no resemblance at all to our previously developed Eq. 1, but actually this approximation works rather well down to a meteor zenith angle of 75-80 degrees, after which it “blows up” badly. Figure 4 shows the meteor distance (d) for a meteor at h = 100 km, plotted as a function of meteor zenith angle, using both equations 1, and 2.
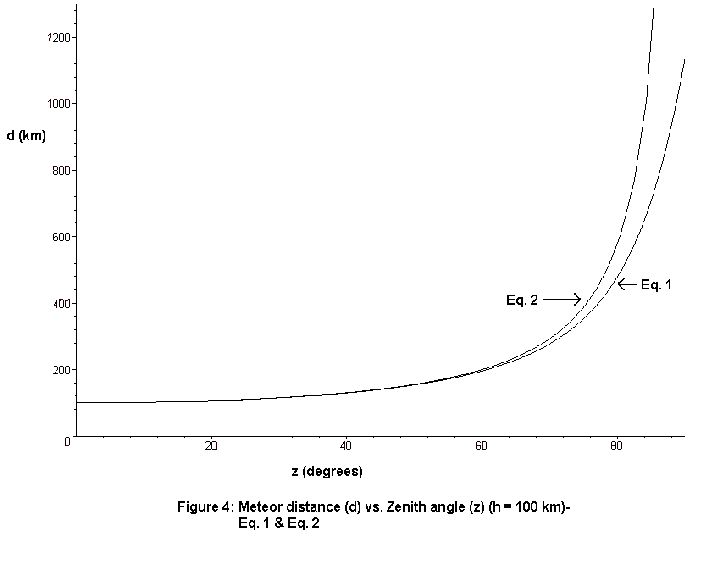
Note that the two equations agree surprisingly well for low zenith angles, but that distances calculated using Eq. 2 begin to deviate significantly from the actual distances (using Eq. 1) for zenith angles greater than 75-80 degrees or so. Thus, meteor correction factors, such as those which correct for shower radiant altitude or meteor magnitudes, developed using Eq. 2 cannot be applied with accuracy for radiant or meteor altitudes below about 10-15 degrees. This should be kept in mind when calculating Zenithal Hourly Rates (ZHR) or other meteor parameters which often utilize this approximation.
Earth Grazing Meteors
One of the more fascinating aspects of our gently curved meteor meniscus is the fact that it will permit the viewing of meteors whose radiant is actually below the horizon of the observer. From Figure 1, it can be seen that a shower radiant which is exactly at the horizon, to either left or right, will still generate meteors which strike our meniscus horizontally, but “illuminating” only 1/2 of our observable sky. Meteors which are seen near the horizon will have some small entry angle into the atmosphere, but those meteors which occur nearly overhead will be travelling almost perfectly horizontal. These grazers can traverse unusually long paths through the atmosphere because they are skimming horizontally through less dense portions of air , rather than penetrating downward to denser layers. These meteors are quite spectacular to observe and can occasionally cover more than 100 degrees of arc for an observer below.
As the shower radiant dips below the horizon, it will, for a time, still be able to illuminate some portion of our meteor meniscus — as long as the entry angle of the meteors into the atmosphere remains at 0 degrees or higher. This permissible region of sky shrinks as the meteor radiant drops, and the resulting meteors will occur at greater and greater distances from the observer. Finally, the shower radiant will reach a critical angle below which it can no further illuminate our observable sky, and the show will be over until the radiant once again begins to rise — with the first possible meteors from the shower occurring when this critical angle is again reached.
Since watching for those beautiful pre-radiant rise grazing meteors is a popular activity among meteor observers, it will be fun to explore this a bit further. I f we hypothesize that our grazer is moving horizontally (or nearly so) directly over it’s local patch of Earth, and further stipulate that it’s midpoint has an altitude of about 100 km, we can use our previous exploration to gain some ideas as to the radiant altitudes and meteor magnitudes necessary for those pre-radiant rise grazers to occur. Note that I am assuming a fast enough shower not to be concerned with zenith attraction, and that meteor altitudes and distances are measured from the midpoint of the meteor’s path. Table 2, below, shows grazing meteor angular altitudes (90 deg – z), distances (km), and magnitude extinctions as a function of radiant altitude, beginning with the radiant critical angle:
Table 2: Grazing Meteor Parameters verses Radiant Altitude
| radiant altitude (deg) | meteor altitude (deg) | meteor distance (km) | magnitude extinction (mag) |
|---|---|---|---|
| -10.1 deg | 0 deg | 1134 km | +7.9 mag |
| -9.1 deg | 1 deg | 1028 km | +7.5 mag |
| -8.3 deg | 2 deg | 934 km | +7.3 mag |
| -7.5 deg | 3 deg | 858 km | +7.0 mag |
| -6.8 deg | 4 deg | 773 km | +6.7 mag |
| -5.7 deg | 6 deg | 649 km | +6.1 mag |
| -4.8 deg | 8 deg | 552 km | +5.6 mag |
| -4.2 deg | 10 deg | 477 km | +5.1 mag |
| -3.0 deg | 15 deg | 352 km | +4.1 mag |
| -2.3 deg | 20 deg | 277 km | +3.3 mag |
| -1.5 deg | 30 deg | 196 km | +2.2 mag |
| -1.0 deg | 40 deg | 154 km | +1.4 mag |
| -0.5 deg | 60 deg | 115 km | +0.5 mag |
| 0.0 deg | 90 deg | 100 km | +0.0 mag |
Based upon these estimations, the minimum radiant altitude at which grazing meteors begin to be possible is about -10 deg, but the meteors are so far away that they must be quite bright to be noticed. A meteor of -4 absolute magnitude would only look like a +4 magnitude meteor at this distance. From -10 deg to -5 deg radiant altitude, the meteors march steadily closer to the observer, with a -2 absolute magnitude meteor looking like a +3.3 magnitude meteor when the radiant is at -5 deg altitude. However, the really giant strides in closing the meteor distances down to more common ranges (with little magnitude extinction) occur during the last 5 degrees of radiant rise. This should be the time in which the majority of long grazers are seen, and this is confirmed by Bob Lunsford in that he has also recommended this time frame based simply on his own experience. It should be kept in mind, however, that even for relatively high ZHR showers, pre-radiant rise grazing meteors are quite infrequent, with perhaps only 1 or 2 visible on the night of a shower maximum. Nonetheless, these jewels are certainly worth getting out an extra half-hour or so before radiant rise to look for.
Last updated: July 25, 2000 at 1500 UTC
 American Meteor Society
American Meteor Society